Beginner’s Guide to Sliding Window Algorithm in Programming?

Do you also struggle to find efficient solutions while solving array or string problems? Or do you often find yourself stuck on competitive programming problems like “What is the maximum sum of a subarray?” or “Find the longest substring with non-repeating characters”? If yes, then you’re not alone!

The Sliding Window Technique, as it refers to the process of solving this kind of a problem, significantly reduces the amount of idle calculations one would otherwise face. In the following section, we will see the purpose of the algorithm in question, and what are its benefits in terms of searching for better solutions.

Sliding Window Algorithm Definition

The sliding window approach is a technique used in solving problems which enables you to limit two for loops into a single for loop. Hence the time complexity of a given problem can be brought down to O(n)

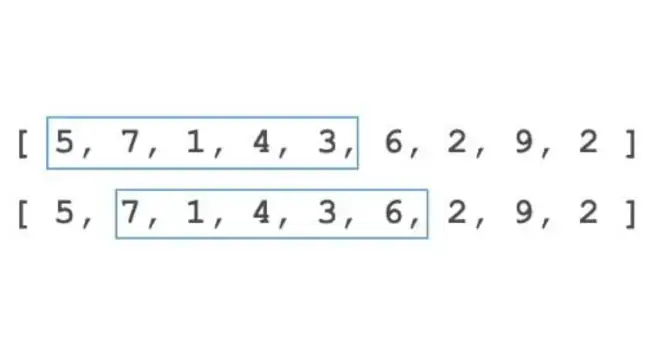
Types of Sliding Windows

1. Fixed-size Window

A sliding window of fixed size has a length fixed in advance which does not change while it “slides” over the array or string, one element at a time. This type of window is particularly useful when the problem requires you to work with subarrays or, in this case, substrings of a predetermined length.

How it Works

• Imagine you’re given an array, and you need to find the maximum sum of all subarrays of length k.
• With a fixed-size window, you start by calculating the sum of the first k elements.
• Then, instead of recalculating the entire sum for the next window, you “slide” the window by one element:
  • Subtract the element that’s leaving the window (the one at the beginning).
  • Add the new element that’s entering the window (the one at the end).

Example

Consider the array [1, 3, 5, 7, 9] and k = 3 (the window length):

• The first window (fixed size) is [1, 3, 5], with a sum of 1 + 3 + 5 = 9.
• Slide one position to [3, 5, 7], sum becomes 3 + 5 + 7 = 15.
• Slide again to [5, 7, 9], sum becomes 5 + 7 + 9 = 21.

Using a fixed-size sliding window saves time compared to recalculating each subarray’s sum from scratch.

Common Use Cases

• Calculating the maximum or minimum sum of a subarray of a fixed length.
• Finding the average of all subarrays of a given length.

2. Variable-size Window

In a variable-size sliding window, there is a possibility of increasing or decreasing the length of the window based on certain factors. This is the case when one is faced with problems needing to satisfy certain conditions such as obtaining a fixed sum or containing different kinds of characters.

How it Works

• The window starts with an initial length but changes as needed:
  • Expand the window by adding elements until the desired condition (e.g., reaching a target sum) is met.
  • Shrink the window by removing elements if the condition is no longer met (e.g., sum exceeds the target).
• This allows the window to adapt its length to fit the conditions, moving start and end pointers dynamically.

Example:

Let’s say you need to find the smallest subarray whose sum is at least S = 15 in the array [2, 1, 5, 2, 3, 2]:

1. Start with a window that expands by adding elements until the sum is ≥ 15.
2. If the sum exceeds 15, shrink the window from the start to find the smallest possible subarray.

Common Use Cases:

• Finding the shortest subarray that meets a target sum.
• Locating the longest substring with unique characters.

What Is the Sliding Window Algorithm? 

The essential concept of the sliding window method is to convert two loops into one. Here are some essential pointers for recognizing problems that can be solved using a sliding window technique:

• The problem examined will involve an array and lists or strings of some kind.
• It will ask to locate subranges in the provided array that would yield the longest, the shortest, or target portions of a string.
• The principle involved here is primarily on the longer or shorter but adequately defined sequences of ‘something.

Let’s say that if you have an array like below:

A sliding window of size three would run over it like below

In my opinion, the sliding window algorithm cannot be classified as an algorithm since it is, rather, a technique that can be utilized in various algorithms.

Steps to Solve a Problem Using the Sliding Window Algorithm

1. Identify If Sliding Window Fits the Problem

• Firstly, assess whether the question pertains to contiguous (next-adjacent) objects in a linear array or string.

• Those variations where it is required to calculate the highest supplementary figure within a fixed width of the array, or find high length substrings devoid of any repeating character, or the smallest subarray satisfying any given condition for example maximum sum of elements in that subarray are particularly suited for Sliding Window technique.

2. Determine the Type of Sliding Window (Fixed-size or Variable-size)

There are two main types

• Fixed-size Window: The window has a set length, which doesn’t change. This is useful for problems that ask for a specific number of elements.
• Variable-size Window: The window length changes as needed. For example, if the goal is to find a subarray that meets a certain condition (like reaching a sum), the window might expand or shrink.

3. Set Up Initial Pointers and Values

• Use pointers like start and end to track the beginning and end of your window.
• Set up any variables needed to calculate the result, such as current_sum (to track the sum of elements in the window) or max_length (for finding the longest subarray).

4. Initialize the First Window (For Fixed-size Windows)

• If you’re working with a fixed-size window, start by calculating the sum or another required value for the first part of the array that fits the window size. This is your starting point.
• For example, if the window size is 3, find the sum of the first 3 elements and use this as your initial sum.

5. Expand and Adjust the Window

For Fixed-size Windows:

• Slide the window one element at a time across the array.
• As you slide, subtract the element that’s leaving the window (on the left) and add the new element entering the window (on the right).
• This way, you’re always working with the current window’s elements without recalculating everything from scratch.

For Variable-size Windows:

• Expand the window by moving the end pointer to include more elements.
• Once the window meets the required condition (like the sum reaching a target), shrink the window by moving the start pointer. This keeps the window as small as possible while still meeting the condition.

6. Check for Desired Conditions and Update Results

Whenever you modify the window, verify whether it satisfies the conditions of the problem, such as having a specified total or being composed of distinct characters only.

Modify your result variables accordingly. For example, in case you are trying to find the maximum sum, make sure the current sum is compared against all previously stored sums and save it if it is greater.

7. Continue Until End of Array or String

• Keep sliding the window along the array or string until you reach the end.
• For variable-size windows, continue adjusting the start and end pointers dynamically based on the problem’s condition.

Sliding Window Algorithm Examples With Solutions

1. Maximum Sum of a Fixed-size Subarray

Problem: Given an array of integers and a number k, find the maximum sum of any contiguous subarray of size k.

Solution Using Fixed-size Sliding Window:

1. Calculate the sum of the first k elements (initial window).
2. Slide the window over the array by one position each time:
   • Subtract the element that’s left behind.
   • Add the new element that comes into the window.
3. Track the maximum sum found.

2. Longest Substring Without Repeating Characters

Problem: Given a string, find the length of the longest substring without repeating characters.

Solution Using Variable-size Sliding Window:

1. Use a window that expands until it contains a duplicate character.
2. When a duplicate is found, shrink the window from the left until it becomes unique again.
3. Track the maximum length of any window found during this process

3. Smallest Subarray with Sum Greater Than or Equal to Target

Problem: Given an array of positive integers and a target S, find the length of the smallest contiguous subarray whose sum is greater than or equal to S.

Solution Using Variable-size Sliding Window:

1. Expand the window by adding elements to the current_sum until it’s ≥ S.
2. Once current_sum meets or exceeds S, try to shrink the window from the left to minimize its size.
3. Track the minimum length for any window that meets the condition.

4. Maximum Number of Ones in a Subarray of Length k

Problem: Given a binary array, find the maximum number of 1s in any contiguous subarray of length k.

Solution Using Fixed-size Sliding Window:

1. Calculate the number of 1s in the initial window of length k.
2. Slide the window by one position each time:
   • Subtract the leftmost element.
   • Add the new element on the right.
3. Track the maximum number of 1s found.

Conclusion

The Sliding Window Algorithm is an efficient technique that helps solve array and string problems easily. It reduces time complexity and simplifies complex problems. By using fixed-size and variable-size windows, you can solve problems like maximum sum, longest substring, or smallest subarray with ease.

Understanding and practicing this technique is crucial for enhancing your problem-solving skills.